時間序列(Time Series)🐭

時間序列資料指的是按照時間順序排列的資料點。這些資料通常在每小時、每天、每月等特定的時間間隔上收集，因此我們會在這些固定的時間點上進行觀測和分析。然而，時間序列資料的本質其實更為複雜。

觀測資料是離散的，因為我們通常只能針對特定時間點之間的資料進行分析，而無法直接觀察到這些點與點之間的連續變化。因此，從這個觀點來看，時間序列資料被認為是離散的。

不過，時間的本質是連續的，而在很多應用中，我們會假設資料在這些離散的時間點之間是以某種連續的方式變化。這意味著，雖然我們觀測的是離散的資料點，但在理論和模型上，我們可以考慮資料的連續性來進行分析或預測。

時間序列資料根據具體的應用場景和分析目標，我們可能會在離散和連續的觀點之間進行切換，來更準確地描述和理解時間序列資料的特性。

時間序列分析技術🐮

移動平均(Moving Average)

移動平均透過消除短期波動來表示資料的長期趨勢，下面舉兩種移動平均的型態：

1. 簡單移動平均(Simple Moving Average, SMA)：

簡單移動平均是一種技術指標，它通過設定一個固定的時間區間，計算該區間內的平均值。在金融領域中，常見的應用包括5日均線（週線）、20日均線（月線）、60日均線（季線）等，以此來評估價格走勢。

程式碼如下：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 生成時間序列數據
np.random.seed(42)
dates = pd.date_range('2023-01-01', periods=100)
data = np.random.randn(100).cumsum() + 50
df = pd.DataFrame({'Date': dates, 'Value': data})

# 計算SMA
df['5SMA'] = df['Value'].rolling(window=5).mean()
df['20SMA'] = df['Value'].rolling(window=20).mean()
df['60SMA'] = df['Value'].rolling(window=50).mean()

# 繪製raw data和SMA
plt.figure(figsize=(10, 6))
plt.plot(df['Date'], df['Value'], label='Original Data')
plt.plot(df['Date'], df['5SMA'], label='Simple Moving Average (5 days)')
plt.plot(df['Date'], df['20SMA'], label='Simple Moving Average (20 days)')
plt.plot(df['Date'], df['60SMA'], label='Simple Moving Average (60 days)')
plt.title('Simple Moving Average')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.grid(True)
plt.show()

輸出結果如下：

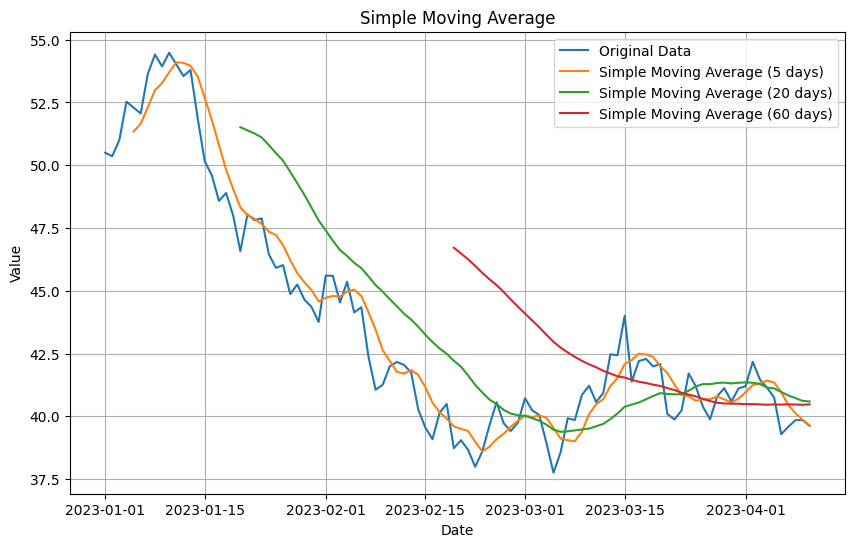
2. 加權移動平均(Weighted Moving Average, WMA)

加權移動平均是在移動平均的基礎上為每個資料點設定權重。通常，距離當前時間越近的資料點會被賦予更大的權重，而距離較遠的資料點則權重較小。

自相關(Autocorrelation Function, ACF)

ACF用於測量時間序列資料在不同時間滯後(lag)之間的相關性。透過ACF可以觀察數據中的週期性和趨勢。當自相關性很高時，表示過去的值對當前值有較強的影響。

程式碼如下：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf

# 生成時間序列數據
np.random.seed(0)
data = np.random.randn(100).cumsum()

# 繪製ACF圖
plot_acf(data, lags=30)
plt.title('Autocorrelation Function (ACF)')
plt.show()

輸出結果如下：

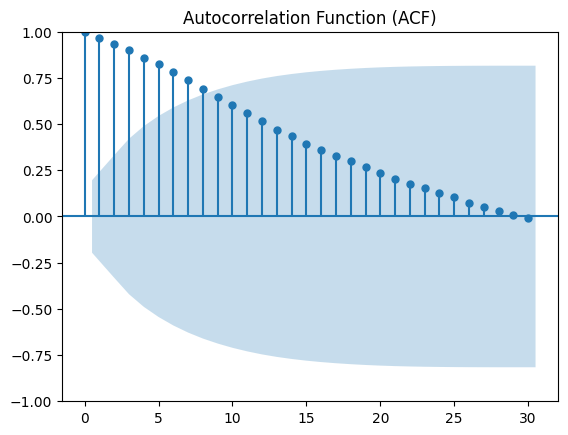
在ACF圖中，每個條形代表不同lag時間下的自相關係數。條形越高，表示該滯後時間下的自相關性越強。如果自相關性在某個滯後時間後迅速下降，這意味著數據中的影響在該時間範圍內已經消失。

時間序列分析的應用🐯

時間序列分析在各個領域都有廣泛的應用，不管是在金融、經濟學和氣象學等領域，能夠有效地幫助預測未來趨勢，制定決策。

1. 金融：股價預測

在金融領域，時間序列分析廣泛應用於股價預測。投資者可以通過分析過去的股票價格和交易量來預測未來的股價走勢。這些預測可以幫助投資者在最佳時機進行買賣，從而獲取更高收益。

2. 經濟學：GDP增長率預測

在經濟學中，時間序列分析被用來預測國家或地區的經濟指標，如GDP增長率、通貨膨脹率、失業率等。這些預測為政府制定經濟政策提供了重要的參考依據，有助於穩定和促進經濟成長。

3. 氣象學領域：天氣預測

在氣象學中，時間序列分析的應用包括天氣預測、氣候變化趨勢分析等。通過分析歷史氣象數據（如溫度、降水量、風速等），可以預測未來的天氣情況，這對農業、交通和日常生活具有重要意義。

題外話😂

時間過得很快，已經堅持了兩週多的鐵人賽，雖然過程很辛苦，下班回家吃飽飯後就要開始趕工，但這段時間也讓我學到了很多👍